20世纪被称作第三次科技革命的重要标志之一的计算机的发明与应用,其运算模式正是二进制,二进制是计算技术中广泛采用的一种数制。二进制数据是用0和1两个数码来表示的数。它的基数为2,进位规则是“逢二进一”,借位规则是“借一当二”,由18世纪德国数理哲学大师莱布尼兹发现。直到20世纪30年代中期,美国科学家冯.诺依曼大胆地提出:抛弃十进制,采用二进制作为数字计算机的数制基础。从此以后,计算机的研究飞速发展,人们把冯.诺依曼的这个理论称为”冯.诺依曼体系机构。直到现在当前的计算机系统使用的基本上是二进制系统。
十进制
十进制计数法是相对二进制计数法而言的,是我们日常使用最多的计数方法(俗称“逢十进一”),它的定义是:“每相邻的两个计数单位之间的进率都是十”的计数方法,叫做“十进制计数法”。
二、转换方法
十进制数转换为二进制数时,由于整数和小数的转换方法不同,所以先将十进制数的整数部分和小数部分分别转换后,再加以合并。
1、十进制整数转换为二进制整数
案例1:

注:十进制转二进制方法:
十进制整数转换为二进制整数采用”除2取余,逆序排列“法。具体做法是:用2去除十进制整数,可以得到一个商和余数;再用2去除商,又会得到一个商和余数,如此进行,直到商为0时为止,然后把先得到的余数作为二进制数的低位有效位,后得到的余数作为二进制数的高位有效位,依次排列起来。也叫“倒序取余”
案例2:
如:255(十进制)=11111111(二进制)
255/2=127=====余1
127/2=63======余1
63/2=31=======余1
31/2=15=======余1
15/2=7========余1
7/2=3=========余1
3/2=1=========余1
1/2=0=========余1
案例3:
如:789=1100010101
789/2=394.5 =1 第10位
394/2=197 =0 第9位
197/2=98.5 =1 第8位
98/2=49 =0 第7位
49/2=24.5 =1 第6位
24/2=12 =0 第5位
12/2=6 =0 第4位
6/2=3 =0 第3位
3/2=1.5 =1 第2位
1/2=0.5 =1 第1位
2、十进制小数转二进制小数
十进制小数转换成二进制小数采用”乘2取整,顺序排列”法。具体做法是:用2乘十进制小数,可以得到积,将积的整数部分取出,再用2乘余下的小数部分,又得到一个积,再将积的整数部分取出,如此进行,直到积中的小数部分为零,此时0或1为二进制的最后一位。或者达到所要求的精度为止。
然后把取出的整数部分按顺序排列起来,先取的整数作为二进制小数的高位有效位,后取的整数作为低位有效位。
注:十进制小数转二进制
案例1:如 0.625=(0.101)B
0.625*2=1.25======取出整数部分1
0.25*2=0.5========取出整数部分0
0.5*2=1==========取出整数部分1
案例2 如 0.7=(0.1 0110 0110…)B
0.7*2=1.4========取出整数部分1
0.4*2=0.8========取出整数部分0
0.8*2=1.6========取出整数部分1
0.6*2=1.2========取出整数部分1
0.2*2=0.4========取出整数部分0
0.4*2=0.8========取出整数部分0
0.8*2=1.6========取出整数部分1
0.6*2=1.2========取出整数部分1
0.2*2=0.4========取出整数部分0 [1]

十进制整数转换为二进制整数原理
众所周知,二进制的基数为2,我们十进制化二进制时所除的2就是它的基数。谈到它的原理,就不得不说说关于位权的概念。某进制计数制中各位数字符号所表示的数值表示该数字符号值乘一个与数字符号有关的常数,该常数称为 “位权 ” 。位权的大小是以基数为底,数字符号所处的位置的序号为指数的整数次幂。十进制数的百位、十位、个位、十分位的权分别是10的2次方、10的1次方、10的0次方,10的-1次方。二进制数就是2的n次幂。
按权展开求和正是非十进制化十进制的方法。
下面我们开讲原理,举个十进制整数转换为二进制整数的例子,假设十进制整数A化得的二进制数为edcba 的形式,那么用上面的方法按权展开, 得
A=a(2^0) b(2^1) c(2^2) d(2^3) e(2^4) (后面的和正是化十进制的过程)
假设该数未转化为二进制,除以基数2得
A/2=a(2^0)/2 b(2^1)/2 c(2^2)/2 d(2^3)/2 e(2^4)/2
注意:a除不开二,余下了!其他的绝对能除开,因为他们都包含2,而a乘的是1,他本是绝对不包含因数2,只能余下。
商得:
(2^0) c(2^1) d(2^2) e(2^3),再除以基数2余下了b,以此类推。
当这个数不能再被2除时,先余掉的a位数在原数低,而后来的余数数位高,所以要把所有的余数反过来写。正好是edcba
十进制小数转换为二进制小数原理
关于十进制小数转换为二进制小数
假设一十进制小数B化为了二进制小数0.ab的形式,同样按权展开,得
B=a(2^-1) b(2^-2)
因为小数部分的位权是负次幂,所以我们只能乘2,得
2B=a b(2^-1)
注意a变成了整数部分,我们取整数正好是取到了a,剩下的小数部分也如此。
值得一提的是,小数部分的按权展开的数位顺数正好和整数部分相反,所以不必反向取余数了。
三、内容扩展
在我们的生活中除了二进制之外还有没有其他的数制呢?其实在我们的生活中还有很多数制存在,比如我们的时间1小时有60分,逢60进1,也就是六十进制,比如1星期有7天,这是7进制,再比如旧时的秤一斤有16两,他们使用的是十六进制,所以有了“半斤八两”的说法。由于二进制数是计算机进行计算的基本进制,它能方便地通过0和1两种状态表示各种数值,这使得逻辑电路的设计简洁。八进制和十六进制对二进制的转换十分方便,同时又能将较大的二进制数以较短的字数来表示,便于人们书写和记录,所以使用八进制和十六进制来表达二进制数。下面我们就来说说八进制、十六进制和十进制数之间的转换。
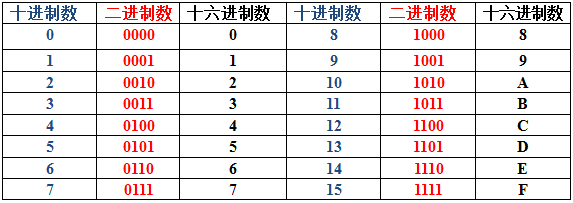
1、二进制和十六进制转换
如果把四位二进制数看作一个整体,那么刚好与十六进制的一个数对应。因此,如果从二进制数的最低位起向高位每四位一组(不足四位时补0),再把每组对应为十六进制数码,就可以将二进制数转化成十六进制数了
案例1:(10111101010)= 0101 1110 1010 =5EA
反过来,若将十六进制的每个数码写成四位的二进制数(不足四位时补0),就将十六进制数转化成二进制数啦
案例2:(1A2B)=0001 1010 0010 1011
案例3:(ABCD)=1010 1011 1100 1101
2、八进制和十进制的转换
案例1:八进制数56转换为十进制数
(56)8 =5*81 5*80 =40 5=45
案例2: 十进制数转换为八进制数
8|79 …… 7
8|9 …… 1
8|1 …… 1↑
得出结果为:余数取反法,即结果为117